Vous trouverez ci-dessous les devoirs pour les 3^e.

Ces devoirs seront sous forme d’exercices à réaliser individuellement ou de dossiers à réaliser en groupe de 2 ou 3 (selon les consignes).

 

Évaluation des devoirs

L’évaluation de ces devoirs s’effectuera selon les critères suivants :

• Soin/Présentation : le travail doit être réalisé et présenté avec soin
• Rédaction/Calculs : la solution doit être rédigée en présentant des explications et ses raisonnements, ainsi que les étapes des calculs incorporées dans ses explications
• Utilisation de ses connaissances : résultats du cours de 3^e ou des années antérieures

Et pour chaque critère, un niveau à indiquer : D : débutant, A : apprenti, C : confirmé, E : expert.

Chaque devoir sera réalisé sur une feuille grand format. La 1^re page comprendra le prénom, le nom et la classe (pour les dossiers, il y aura les noms des élèves du groupe) ainsi qu’un espace d’environ 7 cm réservé à votre auto-évaluation selon les critères ci-dessus.

 

Devoir n°1

2 exercices : bien indiquer les étapes de calculs.
Solutions à rédiger de façon détaillée sur une grande feuille.
Auto-évaluation : voir les critères ci-dessus.

Exercice 1 :
Calculer :
$ A = \dfrac{2}{3} + \dfrac{4}{7} \qquad B = \dfrac{5}{12}-\dfrac{4}{3} \qquad C = \dfrac{5}{13}+2 \qquad D = \dfrac{2}{5} \times \dfrac{7}{12} $
$ E = 8 \times \dfrac{4}{64} \qquad F = \dfrac{3}{4} \div \dfrac{5}{2} \qquad G = \dfrac{18}{5} \div 8 \qquad H = \dfrac{5}{7} \times \dfrac{2}{7} $

Exercice 2
Calculer :
$ A = \dfrac{9}{11} + \dfrac{5}{11} \div \dfrac{7}{4} \qquad B = \dfrac{\left(\dfrac{9}{11} - 5 \right)}{\dfrac{11}{7}} \qquad C = \dfrac{48 \times 10^9 \times 7 \times 10^{-5}}{28 \times 10^{-2} \times 3 \times 10^3} $
Donner l’écriture scientifique de C.

 

Devoir n°2

4 exercices : bien indiquer les étapes de calculs.
Solutions à rédiger de façon détaillée sur une grande feuille.
Auto-évaluation : voir les critères ci-dessus.

Exercice 1 :
Calculer :
$ A = \dfrac{5}{6} - \dfrac{7}{6} \times \dfrac{1}{14} + \dfrac{2}{3} \qquad B = \dfrac{10^8 \times 10^{-5}}{10^{7}} \times \left(10^{-1}\right)^3 $

Exercice 2 :
Résoudre : $ \qquad \dfrac{3}{5} = \dfrac{8}{x} $

Exercice 3 :
1) Donner l’écriture scientifique de $ C = 314,2 \times 10^{-3} $ et de $ D = 0,72 \times 10^{4} $

2) Donner l’écriture décimale de $C$ et de $D$.

Exercice 4 :
$ E = \dfrac{2 + \dfrac{3}{4}}{\dfrac{3}{4} - 5} $ ${} \qquad {}$ Démontrer que $ E = \dfrac{-11}{17} $

 

Devoir n°3

1 exercice (énoncé sur le cahier Sésamath).
Solution à rédiger de façon détaillée sur une grande feuille.
Auto-évaluation : voir les critères ci-dessus.

Exercice : n°3 page 74
pour la partie d., à l’aide du rapporteur, mesurer l’angle $\widehat{ASO}$ à partir du triangle $SAO$ tracé en vraie grandeur. Le calcul de cet angle sera possible lorsque vous aurez étudié la trigonométrie (chapitre 7).

 

Devoir n°4

2 exercices : solutions à rédiger de façon détaillée sur une grande feuille.
Auto-évaluation : voir les critères ci-dessus.

Exercice 1 : n°3 page 89
indication : utiliser les cas d’égalité des triangles.

Exercice 2 : $AB$ = $6 \, cm$, $BC$ = $8 \, cm$ et $CA$ = $10 \, cm$
a) Construire le triangle $ABC$.
b) Démontrer que $ABC$ est rectangle en $B$.

 

Devoir n°5

1 exercice (énoncé sur le cahier Sésamath).
Solution à rédiger de façon détaillée sur une grande feuille.
Auto-évaluation : voir les critères ci-dessus.

Exercice : n°8 page 16

 

Devoir n°6

2 exercices (énoncés sur le cahier Sésamath).
Solutions à rédiger de façon détaillée sur une grande feuille double.
Auto-évaluation : voir les critères ci-dessus.

Exercice 1 : n°11 page 108

Exercice 2 : n°9 page 112

 

Devoir n°7

2 exercices : solutions à rédiger de façon détaillée sur une grande feuille.
Auto-évaluation : voir les critères ci-dessus.

Exercice 1 :
Le triangle $ABC$ est tel que $AB$ = $5 \, cm$, $\widehat{BAC}$ = $30^\circ$ et $\widehat{ABC}$ = $60^\circ$.
a) Construire le triangle $ABC$.
b) Démontrer que $ABC$ est un triangle rectangle.
c) En admettant que $BC$ = $2,5 \, cm$, calculer $AC$.
Facultatif : comment peut-on expliquer que $BC$ = $2,5 \, cm$ ?

Exercice 2 :
Le triangle $ABC$ est tel que $AB$ = $4 \, cm$, $BC$ = $4,2 \, cm$ et $CA$ = $5,8 \, cm$
a) Construire le triangle $ABC$.
b) Démontrer que $ABC$ est un triangle rectangle.
c) Mesurer $\widehat{BCA}$ et $\widehat{BAC}$.

 

Devoir n°8

1 exercice (énoncé sur le cahier Sésamath).
Solutions à rédiger de façon détaillée sur une grande feuille simple.
Auto-évaluation : voir les critères ci-dessus.

Exercice : n°3 page 27

 

Devoir n°9

2 exercices (énoncés sur le cahier Sésamath).
Solutions à rédiger de façon détaillée sur une grande feuille double.
Auto-évaluation : voir les critères ci-dessus.

Exercice 1 : n°15 page 56

Exercice 2 : n°6 page 28

 

Devoir n°10

Le devoir est en téléchargement ci-dessous. Les données recueillies dans ce devoir serviront pour le cours sur les probabilités.

L’utilisation d’un tableur est recommandée pour ce devoir : vous pourrez joindre à votre copie les tableaux et graphiques obtenus (ne pas oublier les légendes).

NB : dans les divers tableaux, ne pas oublier une colonne pour indiquer le total.

Rédigez la démarche avec soin et précision sur une grande feuille double.
Et n’oubliez pas de vous évaluer en utilisant les mêmes critères que les devoirs précédents.

 

Devoir n°11

2 exercices
Solutions à rédiger de façon détaillée sur une grande feuille simple.
Auto-évaluation : voir les critères ci-dessus.

Exercice 1 :
On considère le programme de calcul :

1. Choisir un nombre
2. Prendre le carré de ce nombre
3. Ajouter le triple du nombre de départ
4. Ajouter 2

1. Montrer que si on choisit 1 comme nombre de départ, le programme donne 6 comme résultat.
2. Quel résultat obtient-on si on choisit −5 comme nombre de départ ?
3. On appelle $x$ le nombre de départ, exprimer le résultat en fonction de $x$
4. Montrer que ce résultat peut aussi s’écrire sous la forme $(x + 2)(x + 1)$ pour toutes les valeurs de $x$.
5. La feuille du tableur suivante regroupe des résultats du programme.

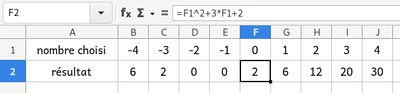
a) Quelle formule a été écrite dans la cellule B2 avant de l’étendre jusqu’à la cellule J2 ?
b) Trouver les valeurs de $x$ pour lesquelles le programme donne 0 comme résultat.

Exercice 2 :
Juliette a écrit le programme ci-dessous.

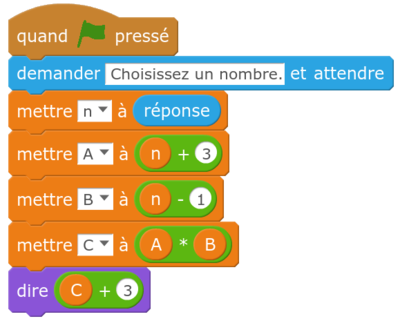
a) Recopier et compléter le tableau en indiquant les valeurs obtenues à chaque étape.

Nombre choisi	2	– 1	8
A
B
C
Nombre annoncé	8

b) On choisit $n$ pour nombre de départ.
Donner l’expression du nombre annoncé en fonction de $n$.
Développer et simplifier cette expression.

 

Devoir n°12

2 exercices (énoncés sur le cahier Sésamath).
Solutions à rédiger de façon détaillée sur une grande feuille simple.
Auto-évaluation : voir les critères ci-dessus.

Exercice 1 : n°14 page 41

Exercice 2 : n°8 page 101

 

Devoir n°13

1 exercice (énoncé sur le cahier Sésamath).
Solutions à rédiger de façon détaillée sur une grande feuille double.
Auto-évaluation : voir les critères ci-dessus.

Exercice 1 : n°1 page 69

 

Devoir n°14

2 exercices (énoncés sur le cahier Sésamath).
Solutions à rédiger de façon détaillée sur une grande feuille double.
Auto-évaluation : voir les critères ci-dessus.

Exercice 1 : en préparation…

Exercice 2 : en préparation…