Accueil > Disciplines > Mathématiques > ■ Cours de M. Suquet > Cours de 4e > Devoirs pour les 4e

Devoirs pour les 4e

par Michel Suquet

 

Vous trouverez ci-dessous les devoirs pour les 4e.

Évaluation des constructions

Lorsqu’ il s’agit de constructions géométriques, elles seront évaluées à partir de 3 critères :

  • Soin/Présentation : le travail doit être réalisé et présenté avec soin
  • Précision : la construction doit être précise
  • Réalisation : la construction doit être complète et l’auto-évaluation effectuée

Et pour chaque critère, un niveau à indiquer : D : débutant, A : apprenti, C : confirmé, E : expert.

Chaque construction sera réalisée sur une feuille blanche au format A4 (feuille pour imprimante 70g ou 80g).

Attention : les traits de construction ne doivent pas être effacés.

Évaluation des écrits

Lorsque le devoir n’est pas une construction géométrique, les critères d’évaluation seront les suivants :

  • Soin/Présentation : le travail doit être réalisé et présenté avec soin
  • Rédaction/Calculs : la solution doit être rédigée en présentant des explications et ses raisonnements, ainsi que les étapes des calculs incorporées dans ses explications
  • Utilisation de ses connaissances : résultats du cours de 4e ou des années antérieures

Et pour chaque critère, un niveau à indiquer : D : débutant, A : apprenti, C : confirmé, E : expert.

Chaque devoir sera réalisé sur une feuille à carreaux grand format. La 1re page comprendra le prénom, le nom et la classe ainsi qu’un espace de 7 cm réservé à l’évaluation.

 

devoir n°1

Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.

Construction :

  1. Construire un triangle ODC tel que : DC = 7 cm, OD = 6,5 cm et \widehat{ODC} = 30°
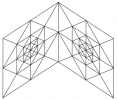
  2. Construire OBA qui est le symétrique de ODC par rapport à O : A et B sont les symétriques respectifs [1] de C et D [2]. Tracer le parallélogramme ABCD.
  3. Soit I, J, K et L les milieux respectifs de [AB], [BC], [CD] et [AD]. Tracer le parallélogramme IJKL ainsi que ses diagonales.
  4. Recommencer l’étape 3 avec les milieux des côtés de IJKL pour obtenir un 3e parallélogramme [3]. Et poursuivez jusqu’à un 6e parallélogramme [4].
  5. Construire le symétrique de la figure obtenue par rapport à la droite (CD).

 

devoir n°2

Rédigez, sur une copie, votre démarche en détail pour présenter votre raisonnement. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice :

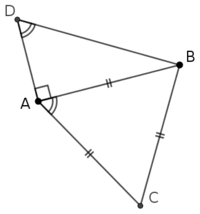
Observer la figure ci-contre.

Calculer \widehat{ABD}.



 

devoir n°3

Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.

Construction :

  1. Tracer un segment [A_1C_1] tel que A_1C_1 = 2 cm.
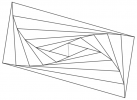
  2. De part et d’autre de [A_1C_1], construire les triangles A_1C_1B_1 et A_1C_1D_1 isocèles respectivement en B_1 et D_1 tels que A_1B_1 = A_1D_1 = 3 cm. A_1B_1C_1D_1 est un losange.
  3. Sur la demi-droite [A_1B_1), placer le point B_2 tel que B_1B_2 = 2 cm avec B_1 entre A_1 et B_2.
  4. De même, sur les demi-droites [B_1C_1), [C_1D_1) et [D_1A_1), placer les points C_2, D_2 et A_2 respectivement.
  5. Tracer le parallélogramme A_2B_2C_2D_2.
  6. Recommencer l’étape 3 sur la demi-droite [A_2B_2) pour obtenir le point B_3, poursuivez avec les étapes 4 et 5 pour obtenir le parallélogramme A_3B_3C_3D_3.
  7. Continuer ainsi jusqu’à obtenir le parallélogramme A_6B_6C_6D_6.

 

devoir n°4

Rédigez, sur une copie, votre démarche en détail pour présenter votre raisonnement. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice :

  1.  ABCD est un parallélogramme et O est l’intersection de ses diagonales avec AB = 6 cm, AD = 4 cm et \widehat{BAD} = 120°.
    Tracer, sur votre copie, le parallélogramme ABCD.
  2.  Par A et C, tracer les perpendiculaires à (BD) : elles coupent (BD) en L et J respectivement. De même, par B et D, tracer les perpendiculaires à (AC) : elles coupent (AC) en K et I respectivement.
  3.  Pourquoi les angles \widehat{LOA} et \widehat{JOC} sont-ils égaux ?
    Pourquoi OA = OC ?
    Démontrer que (AL) et (JC) sont parallèles ; que peut-on en déduire pour les angles \widehat{OAL} et \widehat{OCJ} ?
    Démontrer que les triangles OAL et OJC sont égaux puis en déduire que O est le milieu de [LJ].
  4.  Reprenez ce qui précède avec les triangles ODI et OBK pour démontrer que O est le milieu de [IK].
  5.  En utilisant les résultats précédents, démontrer que IJKL est un parallélogramme.

Revoir le cours de 5e sur les parallélogrammes.

 

devoir n°5

Rédigez, sur une copie, votre démarche en détail pour présenter votre raisonnement. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Énigme des 2 carrés
Comment construire un carré dont l’aire est le double de celle d’un carré de côté 5 cm ?

 

devoir n°6

Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.

Construction :

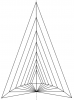
  1. La feuille étant en position portrait, tracer une droite d verticale à peu près centrée : elle servira de support de la base de tous les triangles tracés avec B, C, D, F, H, J, L, N et R sur la droite d.
  2.  Construire les 8 triangles suivants :
    ABC tel que BC = 57 mm, \widehat{ABC} = 20° et \widehat{BCA} = 30°
    EDC tel que DC = 70 mm, \widehat{EDC} = 20° et \widehat{DCE} = 40°
    GFC tel que FC = 85 mm, \widehat{GFC} = 20° et \widehat{FCG} = 50°
    IHC tel que HC = 105 mm, \widehat{IHC} = 20° et \widehat{HCI} = 60°
    KJC tel que JC = 130 mm, \widehat{KJC} = 20° et \widehat{JCK} = 70°
    MLC tel que LC = 160 mm, \widehat{MLC} = 20° et \widehat{LCM} = 80°
    ONC tel que NC = 195 mm, \widehat{ONC} = 20° et \widehat{NCO} = 90°
    SRC tel que RC = 235 mm, \widehat{SRC} = 20° et \widehat{RCS} = 100°
  3. Construire le symétrique de cette figure par rapport à la droite d.
  4. Tracer la ligne brisée [AEGIKMOS] et la ligne brisée symétrique par rapport à d. Tracer [AA’].

 

devoir n°7

Rédigez, sur une copie, votre démarche en détail pour présenter votre raisonnement. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice :

  1. Tracer un carré ABCD de côté 5 cm. Placer un point E sur [AB] tel que AE = 2 cm et un point F sur [BC] de sorte que BF = 2 cm. Tracer [DE] et [AF] puis nommer G leur intersection.
  2. Démontrer que les triangles AED et ABF sont égaux.
  3. En déduire que DE = AF, \widehat{ADE} = \widehat{BAF} et \widehat{AED} = \widehat{BFA}.
  4. Démontrer que \widehat{AED} et \widehat{ADE} sont complémentaires.
  5. En utilisant le triangle AEG et les résultats précédents, démontrer que [DE] et [AF] sont perpendiculaires.

 

devoir n°8

Rédigez, sur une copie, votre démarche en détail pour présenter votre raisonnement. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice :
La Terre tourne sur elle-même autour de son axe Nord-Sud en un jour. En conséquence, une personne qui est sur l’Équateur parcourt une distance d en un jour. On prendra 6 400 km comme valeur approchée du rayon de la Terre.

  1. Donnez une estimation de la valeur de cette distance d. Justifiez.
  2. En déduire une estimation de la vitesse avec laquelle cette personne est entraînée.
    Donnez cette vitesse en km/h puis en m/s.

 

devoir n°9

Rédigez, sur une copie, votre démarche en détail pour présenter votre raisonnement. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice :

  1. Tracer un cercle de centre A et de rayon 4 cm ? Tracer un diamètre [BC] de ce cercle et placer un point D sur ce cercle de sorte que \widehat{BAD} = 30°. Tracer les triangles ABD et BDC.
  2. Calculez \widehat{DAC}
  3. Que peut-on dire des triangles ABD et DAC  ? Justifiez.
  4. En déduire les valeurs de \widehat{ADB} et \widehat{ADC}.
  5. En déduire la valeur de \widehat{BDC} et la nature du triangle BDC.

 

devoir n°10

Rédigez, sur une copie, votre démarche en détail pour présenter votre raisonnement. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice :
Un commerçant propose d’installer des bassins aquatiques de formes carrées dont les bords sont entourés d’une double rangée de carreaux avec n carreaux par côté du bassin. Les carreaux ont aussi une forme carrée.

Voici un schéma pour n = 3 :

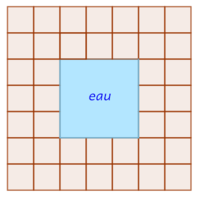
  1. À l’aide de schémas similaires, déterminer le nombre de carreaux nécessaires pour n = 1.
    Même tra­vail pour n = 2 et pour n = 3.
  2. Quelle est la formule exprimant le nombre de carreaux nécessaires en fonction de n ?
    Justifier votre réponse.
  3. Pour un bassin aquatique de côté 1,4 m et avec des carreaux de côté 20 cm, combien faut-il prévoir de carreaux ?

 

devoir n°11

Rédigez, sur une copie, votre démarche en détail pour présenter votre raisonnement. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice :

  1. Dans un repère, placer les points A(8\, ;1), B(6\, ;3) et C(2\, ;−1).
  2. Placer le point D(2\, ;3) et calculer BC.
  3. De même, placer E(8\, ;3) et F(8\, ;−1) puis calculer AB et AC.
  4. Démontrer que ABC est un triangle rectangle.
  5. Calculer l’aire du rectangle CDEF.
  6. Calculer les aires des triangles CDB, BEA et AFC.
  7. En déduire l’aire du triangle ABC.
  8. Soit G le centre du cercle circonscrit au triangle ABC ;
    sans justification, donner les coordonnées du point G et tracer ce cercle.

 

devoir n°12

Rédigez, sur une copie, votre démarche en détail pour présenter votre raisonnement. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice :

  1. Représenter en perspective un cube dont la face du dessous est nommée ABCD et celle du dessus est nommée EFGH.
    Repérer le point S qui est l’intersection des diagonales de EFGH et les milieux I, J, K et L des arêtes [AB], [BC], [CD] et [DA] respectivement. Enfin, repérer le point M qui est l’intersection des diagonales de IJKL.
  2. Quelle est la nature et les éléments du solide SIJKL ?
  3. On sait , pour cette question et les suivantes, que AB = 6 cm.
    Tracer en vraie grandeur la face ABCD et placer les points I, J, K, L et M. Calculer l’aire de IJKL.
  4. Calculer le volume de SIJKL.
  5. Calculer IJ et IS.

 

devoir n°13

Rédigez, sur une copie, votre démarche en détail pour présenter votre raisonnement. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice :

  1. Soit un cercle de centre O et de rayon 5 cm. On considère huit points répartis régulièrement sur ce cercle pour obtenir l’octogone régulier ABCDEFGH.
    Calculer \widehat{AOB}.
  2. Tracer le cercle et le polygone régulier ABCDEFGH.
  3. B est l’image de A par une rotation : donner les éléments d’une telle rotation.
    Quelle est l’image de F par cette rotation ?
  4. Quelle est la nature du triangle AOB ?
    Calculer \widehat{OAB} et \widehat{OBA}.
    En déduire \widehat{ABC}.
  5. D est l’image de A par une rotation : donner les éléments d’une telle rotation.
    Quelle est l’image de F par cette rotation ?
  6. Tracer l’octogone étoilé ADGBEHCF.

 

devoir n°14

Rédigez, sur une copie, votre démarche en détail pour présenter votre raisonnement. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice 1
Écrire les 3 lois de Kolmogorov.

Exercice 2
Les 6 faces d’un dé comportent chacune des lettres du mot CALCUL. On lance au hasard le dé et on regarde la face du dessus.

  1.  Pour cette expérience aléatoire, donner un exemple d’événement de chaque nature : élémentaire, non élémentaire, certain et impossible.
  2.  Quel est l’événement contraire de l’événement « Â obtenir la lettre L  »Â ?

Exercice 3
Un jeu consiste à tirer une boule dans un sac (le sac contient 4 boules rouges, 2 boules vertes et 6 boules bleues). Les boules sont indiscernables au toucher.

  1.  Quel modèle peut-on utiliser ? Justifier.
  2.  Combien d’issues réalisent l’événement « Â tirer une boule rouge ou une boule verte  »Â ? Quelle est la probabilité de cet événement ? Justifier votre réponse.

 

devoir n°15

Rédigez, sur une copie, votre démarche en détail pour présenter votre raisonnement. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice 1
Écrire les 3 lois de Kolmogorov.

Exercice 2
Un dé parfait comporte 6 faces numérotées de 1 à 6. On lance au hasard ce dé et on observe la face du dessus obtenue.

  1.  Quelle est la probabilité d’obtenir la face 2 ? Justifier votre réponse.
  2.  Quelle est la probabilité d’obtenir un nombre multiple de 3 ? Justifier votre réponse.

Exercice 3
Un sac ne contient que des jetons rouges, des jetons bleues et des jetons vertes. On tire au hasard un jeton.
Sachant que la probabilité de tirer un jeton rouge est égale à \frac{1}{4} et que la probabilité de tirer un jeton bleu est égale à \frac{2}{3}, en déduire la probabilité de tirer un jeton vert. Justifier votre réponse.

 

Notes

[1] ce qui signifie que A est le symétrique de C, B est le symétrique de D

[2] ici, il est sous-entendu qu’il s’agit de la symétrie par rapport à O

[3] ne pas oublier ses diagonales

[4] on pourrait poursuivre pour obtenir un dessin en abyme

Portfolio

devoir n°1 devoir n°3 devoir n°5