Théorème

Si deux triangles sont semblables alors leurs côtés sont proportionnels.

Réciproquement, si deux triangles ont leurs côtés proportionnels alors ce sont deux triangles semblables.

Démonstration

– Considérons 2 triangles semblables en nommant $ABC$ le plus petit et $DEF$ le plus grand (s’ils sont égaux, le théorème est évident) de sorte que $\widehat{ABC}=\widehat{EFD}$, $\widehat{BCA}=\widehat{FDE}$ et $\widehat{CAB}=\widehat{DEF}$, comme sur la figure suivante.

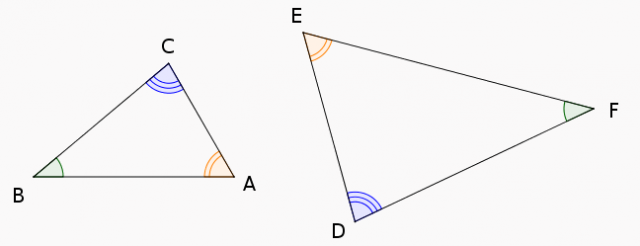
Puisque $\widehat{BCA}=\widehat{FDE}$ [1] on peut déplacer (en le retournant si nécessaire) le triangle $ABC$ pour qu’il s’emboîte dans le triangle $DEF$ comme le montre la figure suivante :

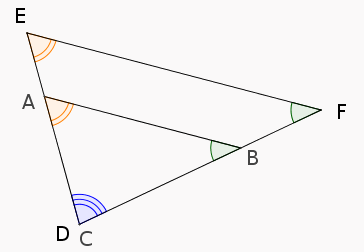
Ainsi, les angles $\widehat{ABC}$ et $\widehat{EFD}$ sont des angles correspondants
or, ils sont égaux
donc les droites $(AB)$ et $(EF)$ sont parallèles.

Dans le triangle $DEF$, $A$ est sur le côté $[DE]$, $B$ est sur le côté $[DF]$ et $(AB)//(EF)$
donc, d’après le théorème de Thalès, les deux triangles $ABC$ et $DEF$ ont leurs côtés proportionnels.CQFD

Plus précisément, on a : $\displaystyle\frac{AC}{ED}=\frac{BC}{FD}=\frac{AB}{EF}$

– Réciproquement, soit deux triangles dont les côtés sont proportionnels ; nommons $ABC$ le plus petit et $DEF$ le plus grand (s’ils sont égaux, la réciproque du théorème est évidente) de sorte que $\displaystyle\frac{AC}{ED}=\frac{BC}{FD}=\frac{AB}{EF}$ $(1)$ :

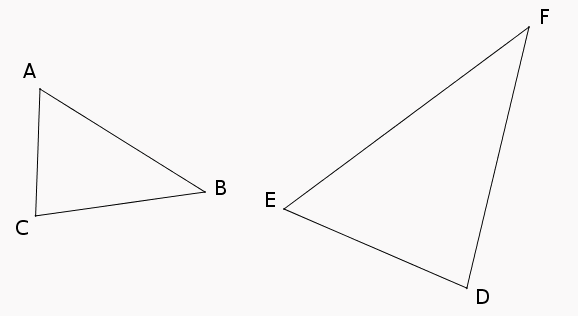
Sur le côté $[DF]$ du triangle $EDF$ [2] , plaçons le point $G$ tel que $DG=CB$ puis traçons la droite passant par G et parallèle à la droite $(EF)$ : elle coupe $[DE]$ en $H$, comme sur la figure suivante :

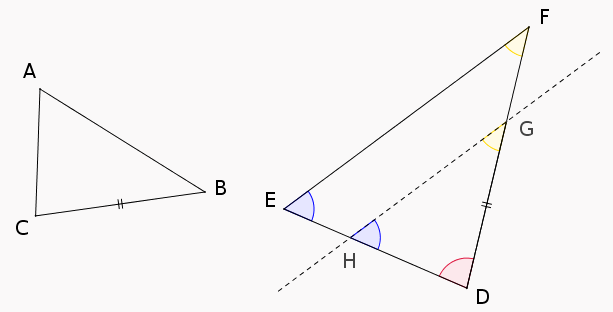
Ainsi, on a des angles correspondants $\widehat{HGD}$ et $\widehat{EFD}$ d’une part, $\widehat{GHD}$ et $\widehat{FED}$ d’autre part.
Or, $(HG)//(EF)$
donc $\widehat{HGD}=\widehat{EFD}$ et $\widehat{GHD}=\widehat{FED}$
et comme $G$ est sur $[DF]$ et $H$ est sur $[DE]$, on a aussi $\widehat{HDG}=\widehat{EDF}$
ce qui montre que les triangles $EDF$ et $HDG$ sont semblables.

Par ailleurs, dans le triangle $EDF$, $H$ est sur $[DE]$, $G$ est sur $[DF]$ et $(HG)//(EF)$
donc, d’après le théorème de Thalès, $\displaystyle\frac{GD}{FD}=\frac{HD}{ED}=\frac{HG}{EF}$
or, $BC=DG$ donc $\displaystyle\frac{BC}{FD}=\frac{HD}{ED}=\frac{HG}{EF}$ (2)
reprenons les égalités $(1)$ ci-dessus : $\displaystyle\frac{AC}{ED}=\frac{BC}{FD}=\frac{AB}{EF}$ $(1)$
par comparaison entre les égalités (1) et les égalités (2), ona : $\displaystyle\frac{AC}{ED}=\frac{HD}{ED}$ et $\displaystyle\frac{AB}{EF}=\frac{HG}{EF}$
donc $AC=HD$ et $AB=HG$, sans oublier que $BC=DG$
ainsi, les triangles $ABC$ et $HGD$ sont égaux.

En résumé, on a montré que, d’une part $HGD$ et $EDF$ sont semblables, et d’autre part $ABC$ et $HGD$ sont égaux,
il en résulte que $ABC$ et $EDF$ sont semblables.CQFD