Devoirs pour les 5^e

par Michel Suquet

Évaluation des constructions

Lorsqu’ il s’agit de constructions géométriques, elles seront évaluées à partir de 3 critères :

Soin/Présentation : le travail doit être réalisé et présenté avec soin
Précision : la construction doit être précise
Réalisation : la construction doit être complète et l’auto-évaluation effectuée

Et pour chaque critère, un niveau à indiquer : D : débutant, A : apprenti, C : confirmé, E : expert.

Chaque construction sera réalisée sur une feuille blanche au format A4 (feuille pour imprimante 70g ou 80g).

Attention : les traits de construction ne doivent pas être effacés.

Évaluation des écrits

Lorsque le devoir n’est pas une construction géométrique, les critères d’évaluation seront les suivants :

Soin/Présentation : le travail doit être réalisé et présenté avec soin
Rédaction/Calculs : la solution doit être rédigée en présentant des explications et ses raisonnements, ainsi que les étapes des calculs incorporées dans ses explications
Utilisation de ses connaissances : résultats du cours de 5^e ou des années antérieures

Et pour chaque critère, un niveau à indiquer : D : débutant, A : apprenti, C : confirmé, E : expert.

Chaque devoir sera réalisé sur une feuille à carreaux grand format. La 1^re page comprendra le prénom, le nom et la classe ainsi qu’un espace d’environ 7 cm réservé à l’auto-évaluation.

DEVOIR 01

Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.

Construction 03T2 (sur une feuille blanche)
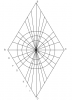
1- Construire un losange $ABCD$ dont les diagonales mesurent 12 cm et 20 cm et se coupent en $O$.
2- Placer sur $[AD]$ les points $E$, $F$, $G$ tels que $AE$ = 2 cm, $EF$ = 1,5 cm et $FG$ = 1 cm
puis les points $I$, $J$, $K$ tels que $DI$ = 2 cm, $IJ$ = 1,5 cm et $JK$ = 1 cm.
3- Joindre, par des segments, les points $E$, $F$, $G$, $I$, $J$ et $K$ au point $O$.
Tracer ensuite les cercles de centre $O$ et de rayons respectivement 2 cm, 3 cm et 4 cm.
4- Continuer le dessin par symétrie axiale par rapport à chacune des diagonales du losange $ABCD$.

DEVOIR 02

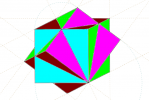
Construction 51T5 (sur une feuille blanche)
1- Tracer un cercle de centre $O$ et de rayon 9 cm.
Sur ce cercle placer deux points $A$ et $B$ tels que $ \widehat{AOB} $ = 72°.
Placer de même avec les points $C$, $D$ et $E$ tels que $ \widehat{BOC} $ = $ \widehat{COD} $ = $ \widehat{DOE} $ = 72°.
Tracer le pentagone régulier $ABCDE$.
2- Placer le point $M$, milieu de $[AB]$ puis le point $N$, milieu de $[AM]$ et le point $P$, milieu de $[MB]$.
Placer de même les points $M_1$, $N_1$ et $P_1$ milieux respectifs de $[AE]$, $[AM_1]$ et $[M_1E]$.
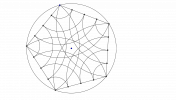
3- À l’intérieur du cercle, tracer l’arc de cercle de centre $A$ et d’extrémités $B$ et $E$.
De même, tracer les arcs de cercle concentriques, de centre $A$, et d’extrémités respectives $P$ et $P_1$, $M$ et $M_1$, $N$ et $N_1$.
4- Recommencer ces constructions (étapes 2 et 3) en prenant successivement $B$, $C$, $D$ et enfin $E$ comme centre des arcs de cercle (Voir le port-folio ci-dessous pour la figure obtenue).

DEVOIR 03

2 exercices : Rédigez, sur une copie, votre démarche en détail pour chaque figure de ces exercices. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation au début de la copie.

Exercices : n°1 page 77 et n°1 page 79
exemple de rédaction : exercices corrigés pages 77 et 79

NB : reproduire les figures sur votre copie.

DEVOIR 04

Exercice 1 : Construire 2 triangles $ABC$ et $DEF$ tels que :
â†’ $AB$ = 5,5 cm, $BC$ = 4,5 cm et $CA$ = 3 cm
â†’ $DE$ = 3 cm, $EF$ = 6 cm et $FD$ = 7 cm

Exercice 2 : Reproduire en vraie grandeur les polygones suivants :

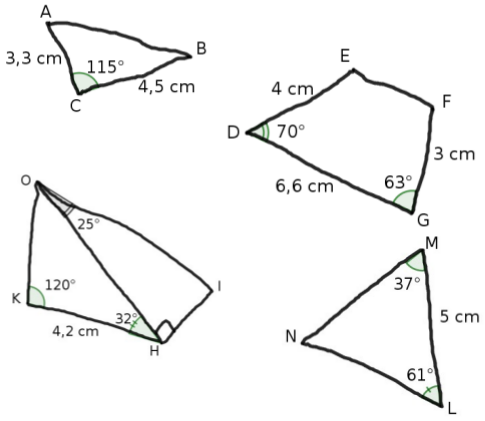
DEVOIR 05

Ce devoir est à réaliser sur la feuille distribuée en classe ou téléchargée (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.

Il s’agit de symétriser chacune des deux figures par rapport à une droite pour la première et par rapport à un point pour la deuxième (document en téléchargement ci-dessous).

DEVOIR 06

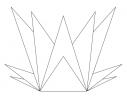
Construction 52T1 (sur une feuille blanche)

1- Tracer un triangle $ABC$ tel que $BC$ = 7 cm, $\widehat{ABC}$ = 70° et $AB$ = 12,5 cm.
2- Tracer le triangle $ACD$ tel que $\widehat{ACD}$ = 88° et $CD$ = 6 cm.
3- Tracer le triangle $ABE$ tel que $\widehat{ EBA}$ = 75° et $BE$ = 2 cm.
4- Tracer le triangle $BCG$ tel que $\widehat{CBG}$ = 57° et $BG$ = 11 cm ; $G$ et $A$ doivent être de part et d’autre de la droite $(BC)$.
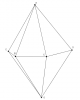
5- Tracer les segments $[EG]$ et $[GD]$.

La figure obtenue est une dipyramide hexagonale en perspective dont six faces sont visibles.

DEVOIR 07

1 exercice : Rédigez, sur une copie, votre démarche en détail pour chaque figure de ces deux exercices. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice : n°1 page 71
exemple de rédaction : exercice corrigé page 71

DEVOIR 08

2 exercices : pour ces exercices, utilisez une copie pour rédiger votre démarche en détail. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice 1 : n°2 page70
aide : exercice corrigé page 70

Exercice 2 : n°3 page 71
aide : une hauteur est perpendiculaire au côté

DEVOIR 09

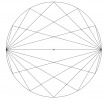
Construction 13T3 (sur une feuille blanche)

Tracer un segment $[AB]$ avec $AB$ = 18 cm puis nommer $I$ son milieu.
Tracer ensuite le cercle de diamètre $[AB]$.
Sur ce cercle, placer les points $C$, $D$, $E$, $F$ et $G$ tels que :
$\widehat{ABC}$ = 15°, $\widehat{ABD}$ = 30°, $\widehat{ABE}$ = 45°, $\widehat{ABF}$ = 60° et $\widehat{ABG}$ = 75°.
Placer les points $C’$, $D’$, $E’$, $F’$ et $G’$ qui sont les symétriques par rapport au point $I$ des points $C$, $D$, $E$, $F$ et $G$ respectivement.
Nommer tous les rectangles obtenus.

DEVOIR 10

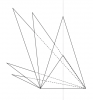
Construction 25T1 (sur une feuille blanche)

Tracer un segment $[BC]$ de 9 cm.
Tracer un triangle $ABC$ isocèle en $A$ avec $AB$ = 15 cm.
Tracer un triangle $SBC$ isocèle en $S$ avec $SB$ = 8 cm.
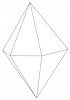
Tracer les 4 triangles suivants (une partie des segments $[FC]$, $[HC]$, $[KC]$ et $[LC]$ sera en pointillés pour que les triangles apparaissent les uns derrière les autres) :
â†’ $FBC$ avec $\widehat{FBC}$ = 96° et $BF$ = 15,2 cm
â†’ $HBC$ avec $\widehat{HBC}$ = 109° et $HB$ = 16,9 cm
â†’ $KBC$ avec $\widehat{KBC}$ = 143° et $BK$ = 8,4 cm
â†’ $LBC$ avec $\widehat{LBC}$ = 154° et $BL$ = 6,3 cm

DEVOIR 11

1 exercice : pour cet exercice, utilisez une copie pour rédiger votre démarche en détail. L’évaluation portera sur le soin, la présentation et la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits et la présentation de la copie. N’oubliez pas votre auto-évaluation.

Exercice : n°3 page 70 + calcul des aires des triangles $BQR$ et $BQC$.
Pour les perfectionnistes : en déduire la distance entre $C$ et $P$.

aide : exercice corrigé page 70 + devoir 03

DEVOIR 12

Exercice : n°4 page 70
astuce : dans un parallélogramme, les côtés opposés ont la même longueur.

aide : exercice corrigé page 70 + devoir 03 et devoir 09

DEVOIR 13

2 exercices : pour ces exercices, utilisez une copie pour tracer avec précision les figures puis rédiger votre démarche en détail. L’évaluation portera sur le soin, la présentation et la qualité des constructions et des explications fournies : voir ci-dessus les détails concernant l’évaluation des constructions et l’évaluation des écrits. N’oubliez pas votre auto-évaluation dans ces deux domaines.

Exercices : n°5 page 86 et n°9 page 87