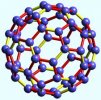
Modèle de sphère
Faire un patron d’une sphère est impossible. Pour vous en convaincre, essayez d’emballer une boule avec une feuille de papier : la feuille de papier se froissera au cours de cette opération.
Par contre, on peut essayer de construire des objets qui approcheront le mieux possible l’idée que l’on se fait d’une sphère.
Le modèle proposé ici a l’avantage de ne nécessiter aucun collage et de pouvoir se monter ou se démonter assez facilement. On pourra le faire avec du carton ou avec du bois.
Voici ce que cela donne une fois l’assemblage fini.

L’objet obtenu est constitué de 6 demi-disques de même rayon et de 6 disques de rayons variables comme cela est expliqué ci-dessous.

Remarque : Dans ces disques et demi-disques, on a pratiqué des fentes qui permettent aux demi-disques de s’emboîter avec les disques.
Réalisation des éléments
Voici le schéma à suivre pour réaliser les disques et demi-disques :
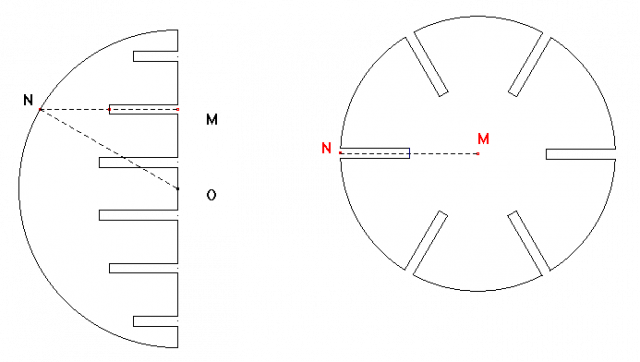
Les rayons des différents disques correspondent à leur position sur les demi-disques. Ainsi, sur chaque demi-disque, on a pratiqué 6 fentes dans lesquelles vont s’emboîter les 6 disques qui auront aussi des fentes pour cela.
Pour chaque demi-disque, le rayon est ON ; c’est le rayon de la sphère à réaliser. À vous de choisir une valeur en fonction de la dimension que vous voulez donner à votre sphère.
Attention : pour les explications suivantes, on prend un rayon de 12 cm : ON = 12 cm. Si vous prenez une valeur différente, vous adapterez les autres dimensions en fonction.
La première chose à faire est de répartir les 6 fentes sur chaque demi-disque. L’écart entre chaque fente sera de 4 cm et il restera 2 cm de part et d’autre.
Ensuite, chaque fente sera la moitié de la longueur MN correspondante, comme sur le schéma. À cette longueur, il va aussi correspondre un des 6 disques qui aura cette longueur MN comme rayon.
Remarque : on peut calculer chaque longueur MN [1] à l’aide du théorème de Pythagore puisque le triangle OMN est rectangle en M. Cependant, il est plus simple de reporter la longueur MN pour obtenir le rayon du disque.
Vous observerez que chaque fente a une longueur qui est la moitié de MN [2]. Les fentes des demi-disques partent du point M mais celles des disques partent du point N. Cela est nécessaire pour l’assemblage des différents éléments.
Sur les disques, les fentes feront des angles de 60° pour obtenir une répartition régulière.
Enfin, chaque fente aura une épaisseur à adapter en fonction de l’épaisseur du carton ou du bois utilisé.
Assemblage des éléments
Pour l’assemblage, on prend un demi-disque et on emboite les 6 disques comme cela :

Ensuite, on emboîte les autres demi-disques au fur et à mesure.






Autres modèles
D’autres modèles de sphère sont possibles. Vous trouverez, ci-dessous, quelques images qui vous donneront une idée de ces possibilités.