Théorème

Pour toute fonction affine $f$, la représentation graphique de $f$ est une droite.

Inversement, pour toute droite $d$ non parallèle à l’axe des ordonnées, $d$ est la représentation graphique d’une fonction affine.

Démonstration

– Considérons une fonction affine $f : x \mapsto ax+b$ avec $a\ne0$ et $b\ne0$ [1]
La représentation graphique de cette fonction est l’ensemble des points de coordonnées $(x ;ax+b)$.
En prenant $x=0$ et $x=1$, on a deux points sur ce graphique cartésien : $B(0 ;b)$ et $A(1 ;a+b)$.

Considérons un point $M$ aligné avec $B$ et $A$, $M$ étant distinct de $B$ et de $A$.
Soient $(x ;y)$ les coordonnées de $M$, les points $I(1 ;0)$, $X(x ;0)$, ainsi que la droite parallèle à l’axe des abscisses et qui passe par B et donc par les points $I’(1 ;b)$ et $X(x ;b)$, comme sur la figure suivante :

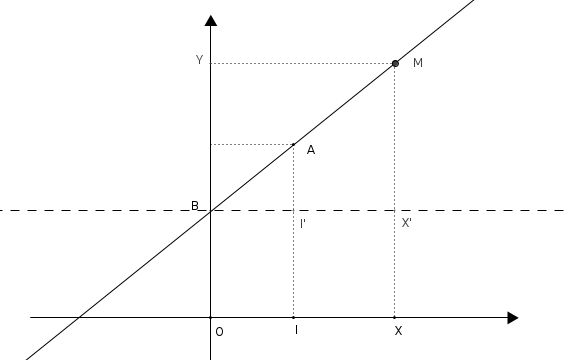
Les droites $(AI)$ et $(MX)$ sont parallèles car elles sont toutes les deux perpendiculaires à l’axe des abscisses ;
avec les alignements $B, I’, X’$ et $B, A, M$, on peut donc utiliser le théorème de Thalès : $\dfrac{BI’}{BX’} = \dfrac{AI’}{MX’}$
Or, on sait que $BI’=OI=1$, $BX’ = BX = x$, $AI’=AI-II’=(a+b)-b=a$ et $MX’=MX-XX’=y-b$
donc $\dfrac{1}{x}=\dfrac{a}{y-b}$ ce qui donne $y-b=ax$ et donc $y=ax+b$

Ainsi, le point $M$ a pour coordonnées $(x ;ax+b)$ [2] :ce qui montre que les points alignés avec $B$ et $A$ sont de coordonnées $(x ;ax+b)$

il en résulte que la représentation graphique de la fonction f est la droite $(BA)$ puisqu’un point est déterminé de façon unique par ses coordonnées. CQFD

– Inversement, considérons une droite $d$ qui ne soit pas parallèle à l’axe des ordonnées.

La droite $d$ n’étant pas parallèle à l’axe des ordonnées a donc un point $A$ dont l’abscisse est 1 ; soit $c$ l’ordonnée de $A$. Considérons aussi le point $B$ de la droite $d$ dont l’abscisse est 0 ; soit $b$ l’ordonnée de $B$. Et posons $a=c-b$ de sorte que les coordonnées de $A$ soient $(1 ;a+b)$.

En prenant un point $M$ de la droite $d$, d’après le raisonnement précédent, le point $M$ a pour coordonnées $(x ;ax+b)$ : il en résulte que la droite $d$ est la représentation graphique de la fonction affine $f$ définie par $x \mapsto ax+b$. CQFD