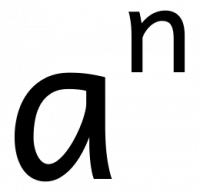
Calculer avec les puissances
Un article détaille les définitions des puissances d’un nombre lorsque l’exposant est un nombre entier, qu’il soit positif, négatif ou nul.
Nous allons donner ici des explications pour les différentes règles de calculs suivantes :
Théorème
Pour tous nombres relatifs non nuls $a$ et $b$
et tous entiers relatifs $n$ et $m$,
– ${a^n}\times{a^m}=a^{n+m}$ $(1)$
– $\frac{a^n}{a^m}=a^{n-m}$ $(2)$
– $\frac{1}{a^{-n}}=a^{n}$ $(3)$ et $\frac{1}{a^{n}}=a^{-n}$ $(4)$
– $(a^n)^m=a^{{n}\times{m}}$ $(5)$
– ${a^n}\times{b^n}=({a}\times{b})^n$ $(6)$
– $\frac{a^n}{b^n}=\left(\frac{a}{b}\right)^n$ $(7)$
Démonstration
La démonstration de chaque formule est assez technique et nous allons procéder par l’examen de différents cas portant sur les exposants.
Dans la plupart des cas, nous procéderons en examinant comment se déroulent ces explications à partir de valeurs particulières qui n’ont qu’un rôle de soutien de la démonstration : on retrouve cela en géométrie avec une figure qui accompagne le raisonnement, même si le rôle de la figure ne se résume pas qu’à cette fonction.
– Considérons un nombre relatif $a$ et des nombres entiers positifs $n$ et $m$ tels que 2 et 5 pour fixer les idées.
En utilisant la définition des puissances, on a ${a^2}={a}\times{a}$ et ${a^5}={a}\times{a}\times{a}\times{a}\times{a}$
donc ${a^2}\times{a^5}={a}\times{a}\times{a}\times{a}\times{a}\times{a}\times{a}$
ce qui montre que ${a^2}\times{a^5}=a^{2+5}$
Ces calculs nous montrent pourquoi le produit de deux puissances revient à ajouter les exposants : il s’agit de compter le nombre de facteurs puisqu’une puissance d’un nombre consiste, lorsque l’exposant est un nombre entier positif, à écrire un produit ayant les mêmes facteurs, les uns à côtés des autres.
On a donc la règle $(1)$ dans le cas des exposants entiers positifs, pour tout nombre relatif $a$.
– Considérons un nombre relatif non nul $a$ et des nombres entiers positifs $m$ et $n$.
Nous avons 3 cas possibles : $n > m$, $n < m$ et $n = m$.
1er cas : $n > m$, par exemple avec $n=5$ et $m=2$
On a $\frac{a^5}{a^2}=\frac{{a^2}\times{a^3}}{a^2}=\frac{a^3}{1}=a^3=a^{5-2}$
2ème cas : $n < m$, par exemple avec $n=2$ et $m=5$
On a $\frac{a^2}{a^5}=\frac{a^2}{{a^2}\times{a^3}}=\frac{1}{a^3}=a^{-3}=a^{2-5}$
3ème cas : $n = m$
On a une fraction dont le numérateur est égal au dénominateur : cette fraction est donc égale à 1.
Or, $a^{n-n}=a^0=1$ donc la règle $(2)$ est vraie aussi dans ce cas
Les calculs précédents nous montrent pourquoi le quotient de deux puissances revient à soustraire les exposants : cela résulte de la simplification effectuée dans chaque cas.
On a donc la règle $(2)$ dans le cas des exposants entiers positifs et pour tout nombre relatif $a$ non nul.
– Considérons un nombre relatif non nul $a$ et des nombres entiers relatifs $m$ et $n$.
On a les cas suivants à examiner : $n>0$ et $m<0$, $n<0$ et $m>0$, $n<0$ et $m<0$ ; sans oublier les cas où $m=0$ ou $n=0$.
1er cas : $n>0$ et $m<0$, par exemple $n=5$ et $m=-2$
on a, par définition, $a^{-2}=\frac{1}{a^2}$
d’où ${a^5}\times{a^{-2}}={a^5}\times\frac{1}{a^2}=\frac{a^5}{a^{2}}=a^{5-2}$
2ème cas : $n<0$ et $m>0$, par exemple $n=-2$ et $m=5$
on a ${a^{-2}\times}{a^5}={a^5}\times{a^{-2}}$ et on se retrouve dans le 1er cas.
3ème cas : $n<0$ et $m<0$, par exemple $n=-2$ et $m=-5$
on a ${a^{-2}\times}{a^{-5}}=\frac{1}{a^2}\times\frac{1}{a^5}=\frac{1}{{a^2}\times{a^5}}=\frac{1}{a^{2+5}}=a^{-(2+5)}=a^{-2-5}$
4ème cas : $m=0$ ou $n=0$, par exemple avec $n=0$
on a $a^0\times{a^m}=1\times{a^m}=a^m=a^{0+m}$
$m=0$ donne des calculs semblables.
Les explications nous montre l’utilisation de la définition de $a^{-n}=\frac{1}{a^{n}}$ lorsque $n > 0$ pour se ramener aux règles $(1)$ et $(2)$ avec des exposants positifs.
La règle $(1)$ permet donc de gagner des étapes de calculs dans ces cas.
On a donc la règle $(1)$ pour tous entiers relatifs $n$ et $m$ et pour tout nombre relatif $a$ non nul.
On peut remarquer que si $m$ et $n$ sont des entiers positifs, la règle est encore vraie dans le cas où $a=0$.
– Considérons un nombre relatif non nul $a$ et un nombre entier $n$ relatif.
Nous allons considérer les deux cas où $n > 0$ et $n < 0$, le 3ème cas $n = 0$ étant très simple à vérifier.
1er cas : $n > 0$, par exemple $n = 7$
On a $\frac{1}{a^{-7}}=\frac{{1}\times{a^7}}{{a^{-7}}\times{a^7}}=\frac{a^7}{a^{-7+7}}=\frac{a^7}{a^0}=\frac{a^7}{1}=a^7$
et $\frac{1}{a^{7}}=a^{-7}$
2ème cas : $n < 0$, par exemple $n = -7$
on a $\frac{1}{a^{-(-7)}}=\frac{1}{a^{7}}=a^{-7}$
et $\frac{1}{a^{-7}}=a^{7}=a^{-(-7)}$
Les calculs précédents nous montrent comment la définition $a^{-n}=\frac{1}{a^{n}}$ donnée dans le cas où $n > 0$ s’étend au cas $n < 0$ et peut s’écrire sous la forme $a^{n}=\frac{1}{a^{-n}}$ pour tout nombre relatif $a$ non nul et pour tout entier relatif $n$.
– Considérons $a$ un nombre relatif non nul , $n$ et $m$ des entiers relatifs.
On a, d’après ce qui précède :
$\frac{a^n}{a^m}={a^n}\times{\frac{1}{a^m}}={a^n}\times{a^{-m}}=a^{n-m}$
On a donc la règle $(2)$ pour tout nombre relatif $a$ non nul et tous entiers relatifs $n$ et $m$.
Cela nous montre encore une fois les liens entre la règle $(1)$ et la règle $(2)$.
– Considérons $a$ un nombre relatif non nul , $n$ et $m$ des entiers relatifs.
On a 4 cas à examiner : $n > 0$ et $m > 0$, $n < 0$ et $m > 0$, $n > 0$ et $m < 0$, $n < 0$, $m < 0$ ; ainsi que le cas où $m = 0$ ou $n = 0$.
1er cas : $n > 0$ et $m > 0$, par exemple $n = 3$ et $m = 4$
$(a^3)^4=a^{3}\times{a^{3}}\times{a^{3}}\times{a^{3}}=a^{3+3+3+3}=a^{{3}\times{4}}$
2ème cas : $n < 0$ et $m > 0$, par exemple $n = -3$ et $m = 4$
$(a^{-3})^4=a^{-3}\times{a^{-3}}\times{a^{-3}}\times{a^{-3}}=a^{-3-3-3-3}=a^{{-3}\times{4}}$
Dans ces deux premiers cas, $(a^n)^4$ est de la forme $b^4$ où $b=a^n$ et en utilisant la définition de $b^4$ et la règle $(1)$, on prouve la règle $(5)$ dans le cas où $m > 0$.
3ème cas : $n > 0$ et $m < 0$, par exemple $n = 3$ et $m = -4$
$(a^3)^{-4}=\frac{1}{(a^3)^{4}}=\frac{1}{a^{3\times4}}=a^{-{3}\times{4}}=a^{{3}\times{(-4)}}$
4ème cas : $n < 0$ et $m < 0$, par exemple $n = -3$ et $m = -4$
$(a^{-3})^{-4}=\frac{1}{(a^{-3})^{4}}=\frac{1}{a^{-3\times4}}=a^{{3}\times{4}}=a^{{-3}\times{(-4)}}$
Dans ces deux derniers cas, l’utilisation de la règle $(4)$ permet de se ramener aux deux premiers cas.
5ème cas : $n = 0$ ou $m = 0$, par exemple $n =0$
$(a^0)^{m}=1^m=1=a^0=a^{0\times{m}}$
calculs semblables avec $m = 0$.
On a donc la règle $(5)$ pour tout nombre relatif $a$ non nul et tous entiers relatifs $n$ et $m$.
On peut remarquer que si $m$ et $n$ sont des entiers positifs, la règle est encore vraie dans le cas où $a = 0$.
– Considérons $a$ et $b$ des nombres relatifs non nul et $n$ un entier relatif.
On a deux cas essentiellement : $n > 0$ et $n < 0$, le cas $n = 0$ étant très simple à vérifier.
1er cas : $n > 0$, par exemple $n = 3$
$a^3\times{b^3}=a\times{a}\times{a}\times{b}\times{b}\times{b}=a\times{b}\times{a}\times{b}\times{a}\times{b}=(a\times{b})^3$
En examinant cette preuve, on voit qu’on a le même nombre de facteurs égaux à $a$ et à $b$ : on peut donc associer $a$ et $b$ pour obtenir un nombre identique de facteur égaux à $a\times{b}$.
On a donc la règle $(6)$ pour tous nombres relatifs non nuls $a$ et $b$ et tout nombre entier positif $n$.
On peut d’ailleurs remarquer que si $a = 0$ ou $b = 0$, la règle $(6)$ est encore vraie si $n > 0$.
2ème cas : $n < 0$, par exemple $n = -3$
$a^{-3}\times{b^{-3}}=\frac{1}{a^3}\times{\frac{1}{b^3}}=\frac{1}{a^3\times{b^3}}=\frac{1}{(a\times{b})^3}=(a\times{b})^{-3}$
On voit donc comment on se ramène au 1er cas en utilisant la règle $(4)$.
Ainsi, on a la règle $(6)$ pour tous nombres relatifs non nuls $a$ et $b$ et tout nombre entier relatif $n$.
– Considérons $a$ et $b$ des nombres relatifs non nul et $n$ un entier relatif.
$\frac{a^n}{b^n}=a^n\times{\frac{1}{b^n}}=a^n\times{b^{-n}}=a^n\times{(b^{-1})^n}=(a\times{b^{-1}})^n=\left(a\times{\frac{1}{b}}\right)^n =\left(\frac{a}{b}\right)^n$
Ainsi, on a la règle $(7)$ pour tous nombres relatifs non nuls $a$ et $b$ et tout nombre entier relatif $n$.
