Théorème

Pour tout triangle, les trois hauteurs se coupent en un même point, ce point est appelé l’orthocentre du triangle.

Démonstration

Soit un triangle $ABC$.

Complétons la figure en traçant les droites parallèles aux côtés du triangle et nommons leurs points d’intersection [1] par $A’$, $B’$ et $C’$, comme cela est indiqué sur la figure suivante :

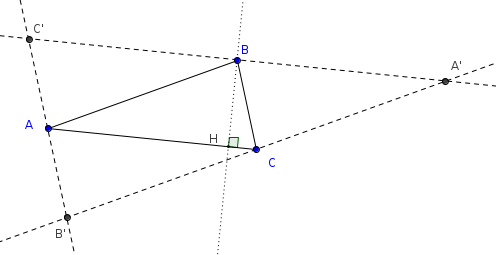
Considérons une des hauteurs du triangle $ABC$, par exemple la hauteur issue de $B$ et désignons par $H$ le pied de cette hauteur, c’est-à -dire le point d’intersection de cette hauteur avec la droite $(AC)$.

Dans le triangle $ABC$, $(BH)$ étant la hauteur issue de B, on a $(BH) \perp (AC)$
et, par construction, $(C’A’)//(AC)$ donc $(BH) \perp (C’A’)$.

Par ailleurs, $(C’A’)//(AC)$ et $(B’A’)//(AB)$ donc $ABA’C$ est un parallélogramme puisque $B$ est sur $(C’A’)$ et $C$ est sur $(B’A’)$.

De même, $(C’A’)//(AC)$ et $(B’C’)//(CB)$ donc $ACBC’$ est un parallélogramme.

$ABA’C$ est un parallélogramme donc $AC=BA’$

$ACBC’$ est un parallélogramme donc $AC=BC’$

donc $BA’=BC’$
et comme $C’$, $B$ et $A’$ sont alignés, $B$ est le milieu du segment $[C’A’]$.

Ainsi, la hauteur issue de B est perpendiculaire à $[C’A’]$ et passe par son milieu : c’est donc la médiatrice de $[C’A’]$.

De raisonnements similaires avec les deux autres hauteurs de $ABC$, il en résulte que les hauteurs de $ABC$ sont les médiatrices de $A’B’C’$.
Or les médiatrices d’un triangle sont concourantes (c’est-à -dire se coupent en un même point)
donc les hauteurs de $ABC$ sont concourantes. CQFD