Que veut dire cette expression dans un texte ?
Voici quelques explications à propos d’expressions souvent employées dans des programmes de construction de figures géométriques.
respectivement, respectifâ‹…ve
Ces mots permettent d’associer 2 à 2 les éléments de 2 listes et évite des répétitions fastidieuses.
Exemple 1 : " $A$, $B$, $C$, $D$ sont les milieux des segments $[EF]$, $[FG]$, $[MN]$ et $[KL]$ respectivement" veut dire que $A$ est le milieu de $[EF]$, $B$ est le milieu de $[FG]$, $C$ est le milieu de $[MN]$ et $D$ est le milieu de $[KL]$.
Exemple 2 : "$d_1$, $d_2$, $d_3$ sont les bissectrices respectives des angles $à‚_1$, $à‚_2$, $à‚_3$" veut dire que $d_1$ est la bissectrice de $à‚_1$, $d_2$ est la bissectrice de $à‚_2$ et $d_3$ est la bissectrice de $à‚_3$.
de part et d’autre
Cela signifie qu’un élément sépare 2 objets : un des objets se trouve d’un côté de l’élément et l’autre objet de l’autre côté.
Exemple : "placer les points $A$ et $B$ de part et d’autre de la droite $d$" est illustré dans la figure ci-dessous. La droite $d$ partage le plan en 2 parties que l’on appelle des demi-plans, le point $A$ est dans un des 1/2-plans et le point $B$ est dans l’autre.
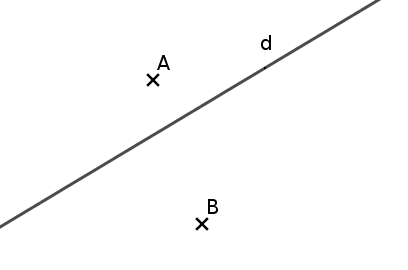
Remarque : le segment $[AB]$ et la droite $d$ ont donc un point d’intersection…
