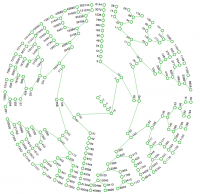
L’énigme de Syracuse
L’idée la plus répandue est que quand un problème est simple, la solution doit être facile à trouver ; mais ce n’est pas vrai.
Pour vous en convaincre, voici un problème facile à comprendre et qui pourtant n’a pas encore reçu de solution.
Le problème est d’utiliser l’algorithme suivant :
prendre un nombre entiersi ce nombre est pair, le diviser par 2, par contre, si ce nombre est impair, le multiplier par 3 puis ajouter 1recommencer avec le nombre entier obtenu
Par exemple, prenons le nombre 5 : 5 étant impair, on le multiplie par 3, ce qui donne 15, et on ajoute 1 pour obtenir 16. On recommence avec le nombre obtenu qui est 16 : 16 étant pair, on le divise par 2 et on obtient 8. On recommence : 8 étant pair, on le divise par 2 et on obtient 4. On recommence : 4 étant pair, on le divise par 2 et on obtient 2. On recommence : 2 étant pair, on le divise par 2 et on obtient 1. On recommence : 1 étant impair, on le multiplie par 3, ce qui donne 3, et on ajoute 1. On obtient 4. On recommence...
Ce que l’on peut résumer par la chaîne suivante :
Dans cet exemple, vous voyez que l’on va obtenir sans arrêt le nombre 1 (plus précisément, le cycle 4→2→1 indéfiniment).
Regardez ce qu’il se passe avec d’autres nombres : que constatez-vous ?
Et oui, vous obtenez à chaque fois le nombre 1, plus ou moins rapidement d’ailleurs.
L’énigme est que personne, pour l’instant, ne sait expliquer pourquoi on obtient 1 au bout d’un certain temps, ni s’il existe un nombre qui ne donnera jamais le nombre 1 quelque soit le temps de fonctionnement de l’algorithme.
