Devoirs pour les 6A et 6E
Voici les textes des devoirs pour les classes de 6A et 6E.
Évaluation des constructions
Lorsqu’ il s’agit de constructions géométriques, elles seront évaluées à partir de 3 critères :
- Soin/Présentation : le travail doit être réalisé et présenté avec soin
- Précision : la construction doit être précise
- Réalisation : la construction doit être complète et l’auto-évaluation effectuée
Et pour chaque critère, un niveau à indiquer : D : débutant, A : apprenti, C : confirmé, E : expert.
Chaque construction sera réalisée sur une feuille blanche au format A4 (feuille pour imprimante 70g ou 80g).
Attention : les traits de construction ne doivent pas être effacés.
Évaluation des écrits
Lorsque le devoir n’est pas une construction géométrique, les critères d’évaluation seront les suivants :
- Soin/Présentation : le travail doit être réalisé et présenté avec soin
- Rédaction/Calculs : la solution doit être rédigée en présentant des explications et ses raisonnements, ainsi que les étapes des calculs incorporées dans ses explications
- Utilisation de ses connaissances : résultats du cours de 6e ou des années antérieures
Et pour chaque critère, un niveau à indiquer : D : débutant, A : apprenti, C : confirmé, E : expert.
Chaque devoir sera réalisé sur une feuille à carreaux grand format. La 1re page comprendra le prénom, le nom et la classe ainsi qu’un espace de 7 cm réservé à l’évaluation.
DEVOIR 01
Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.
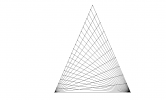
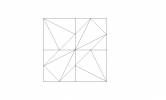
Sur une feuille blanche au format A4 en position portrait, tracer un rectangle de 16 cm de largeur sur 20 cm de longueur.
Sur chaque côté, faire un repère tous les 4 cm et construire ainsi un quadrillage à mailles carrées.
Tracer les diagonales de chacun des carrés obtenus.
DEVOIR 02
Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.
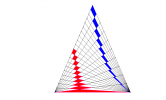
Tracer un carré ABCD de 13 cm de côté.
Sur le côté [AB], en allant du sommet A vers le sommet B, placer le point I à 3 cm de A, le point J à 1 cm de I, le point K à 1 cm de J, le point L à 3 cm de K, le point M à 1 cm de L et le point N à 1 cm de M.
Faire de même sur le côté [DC] qui est opposé au côté [AB].
Relier par des segments chaque point du côté [AB] au point correspondant du côté [DC] : on obtient six segments parallèles à l’intérieur du carré.
Faire les mêmes constructions à partir des segments [AD] et [BC].
DEVOIR 03
Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.
Trace un carré ABCD tel que AB = 18 cm.
Place le milieu E du segment [AB], puis F celui de [BC], G celui de [CD] et H celui de [AD].
Trace les segments [EG] et [FH]Â : ils se coupent en un point que tu nommes O. Trace les diagonales du carré ABCD et vérifie qu’elles passent aussi par le point O.
Place les milieux I et J des segments [EB] et [BF] respectivement(*). Trace le triangle IOJ. Vérifie que IOJ est un triangle isocèle en O.
Place les milieux K et L de [EO] et [HO] respectivement. Trace le triangle AKL. Vérifie qu’il est isocèle.
Prolonge le segment [OJ] jusqu’à ce qu’il coupe le segment [AD] en un point que tu nommes M. Vérifie que M est le milieu de [HD].Fais de même avec le segment [OI] pour obtenir le milieu N de [DG]. Trace [MN].
Le segment [JN] coupe le segment [OF] en un point P. Vérifie que P est le milieu de [OF]. De même, [JN] et [OG] se coupent en R. Trace le triangle PRC. Vérifie que PRC est isocèle en C.
Vérifie que les points M, L, K et I sont alignés. Finis de tracer le quadrilatère IMNJ. Vérifie que tu obtiens un rectangle.
La phrase "Place les milieux I et J des segments [EB] et [BF] respectivement" signifie que I est le milieu de [EB] et J le milieu de [BF].
DEVOIR 04
Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.
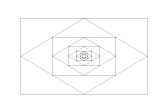
Tracer un rectangle ABCD tel que AB = 20 cm et AD = 12 cm.
Placer les milieux E, F, G et H des segments [AB], [BC], [CD] et [AD] respectivement. Tracer le quadrilatère EFGH. Vérifier que c’est un losange.
Placer les milieux I, J, K et L des côtés [EF], [FG], [GH] et [HE] respectivement. Tracer le quadrilatère IJKL. Vérifier que c’est un rectangle.
Recommencer 5 fois les étapes ci-dessus dans le rectangle IJKL mais sans nommer les milieux des losanges et rectangles obtenus. On obtient un dessin en abyme.
DEVOIR 05
Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.
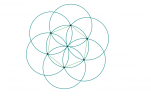
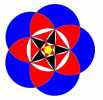
Les rosaces du carré
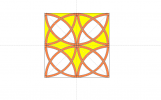
Trace un carré ABCD de côté 9 cm .
Trace ses diagonales [AC] et [BD] qui se coupent en un point que tu appelles O.
Trace le quart de cercle de centre A et d’extrémités B et D.
Trace de même les quart de cercle de centres B, C et D, inscrits dans le carré ABCD.
Trace les demi-cercles de centres A, B, C et D, qui passent par le point O et qui se coupent en des points A’, B’, C’ et D’ : ces points forment un plus grand carré que tu traces. Si tu observes bien, il y a six carrés !
DEVOIR 06
Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.
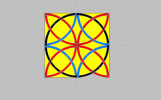
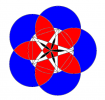
Tracer un carré ABCD de 16Â cm de côté.
E est l’intersection des diagonales du carré ABCD.
Placer les points I, J, K et L milieux respectifs des segments [AB], [BC], [CD] et [DA].
Tracer, à l’intérieur du carré ABCD, des demi-cercles de centre I, J, K et L, tous de rayon 8 cm.
Tracer, à l’intérieur du carré ABCD, des quarts de cercles de centre A, B, C et D, tous de rayon 8 cm.
Faire les mêmes constructions avec un rayon égal à 7,5Â cm.
Tracer les 2 cercles concentriques de centre E et de rayons respectifs 8Â cm et 7,5Â cm.
DEVOIR 07
Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.
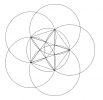
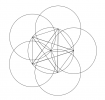
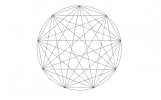
Tracer un cercle de centre A et de rayon 10 cm.
Placer 5 points B, C, D, E et F sur ce cercle tels que $\widehat{BAC}$ = $\widehat{CAD}$ = $\widehat{DAE}$ = $\widehat{EAF}$ = $\widehat{FAB}$ = 72°.
Tracer le pentagone régulier BCDEF inscrit dans le cercle puis le pentagone régulier étoilé BDFCE qui est aussi inscrit dans le cercle.
Attention : pour ce qui suit, ne tracer que la partie des cercles qui ne débordent pas de la feuille A4.
Tracer le cercle de centre B et qui passe par C, le cercle de centre C et qui passe par D, le cercle de centre D et qui passe par E, le cercle de centre E et qui passe par F, le cercle de centre F et qui passe par B. Cela donne une des rosaces du pentagone (rosace-côté).
Dans le port-folio ci-dessous, vous trouverez une autre rosace du pentagone (rosace-centre) que l’on retrouve en coupant une pomme en deux.
DEVOIR 08
Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.
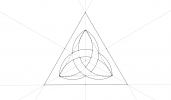
Trace un triangle équilatéral ABC de côté 12 cm .
Appelle I, J et K les milieux des côtés [AB], [BC] et [CA] respectivement.
Trace l’arc de cercle de centre I et d’extrémités A et B et passant par J et K.
Trace de même les arcs de cercle de centre J et K.
Trace les médiatrices de chaque côté du triangle ABC et prolonge-les de 2 cm de part et d’autre. : tu obtiens le point D situé à 2 cm du point J et à l’extérieur du triangle ABC, le point F à 2 cm de K et le point E à 2 cm de I de la même manière.
Trace la perpendiculaire à la droite (AD) et qui passe par D. Fais les même construction à partir des points E et F. Tu obtiens un nouveau triangle équilatéral.
Trace les arcs de cercles, situés à l’intérieur du grand triangle équilatéral, ayant pour centre D, E et F passant respectivement par B et C, A et B, C et A.
DEVOIR 09
Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.
Tracer un cercle de centre A et de rayon 8 cm.
Tracer 2 diamètres perpendiculaires [BC] et [DE] de ce cercle.
Tracer la bissectrice d1 de l’angle $\widehat{BAE}$ : elle coupe le cercle en 2 points F et G avec F qui est dans l’angle $\widehat{BAE}$.
Tracer les bissectrices des angles $\widehat{BAF}$ et $\widehat{FAE}$ .
Tracer le cercle de centre A et de rayon 4 cm : il coupe les 2 dernières bissectrices tracées, en M et en N respectivement.
Tracer les segments [BM], [MF], [FN] et [NE].
Recommencez ces constructions dans les angles $\widehat{EAC}$, $\widehat{CAD}$ et $\widehat{DAB}$ pour obtenir une étoile à 8 branches (polygone étoilé).
DEVOIR 10
2 exercices : Rédigez votre démarche en détail pour ces deux exercices. L’évaluation portera sur la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits.
Exercice 1
Lorsque Dominique fait la vaisselle, quatre assiettes sur dix sont cassées. Après sa fête d’anniversaire, Dominique doit laver les quinze assiettes qui ont été utilisées.
Combien d’assiettes sortiront intactes de cette vaisselle ?
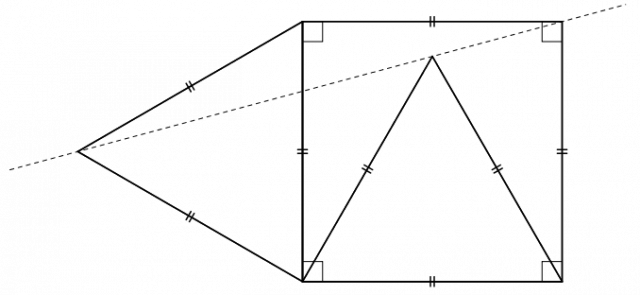
Exercice 2
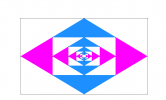
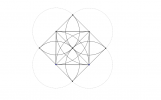
Rédiger un programme de construction de la figure suivante :
DEVOIR 11
Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.
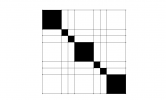
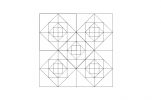
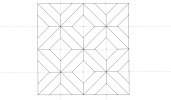
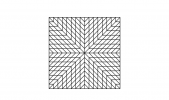
Tracer un carré ABCD de côtés 16 cm. Le partager en 4 carrés identiques.
Partager chaque carré obtenus en 4 carrés identiques et soit AEFG le petit carré qui se trouve dans un coin.
Tracer la diagonale [AF] et repérer les milieux M, N, O et P des côtés [AE], [EF], [FG] et [GA] respectivement. Tracer [MN] et [OP] qui sont parallèles à [AF].
Procéder de même dans les 3 autres petits carrés de manière symétrique par rapport à (EF) et à (FG).
Dans les autres petits carrés, utiliser le motif ainsi obtenu pour paver ABCD.
DEVOIR 12
Il s’agit de symétriser chacune des deux figures par rapport à une droite (document en téléchargement ci-dessous).
Ce devoir est à réaliser sur la feuille distribuée en classe ou téléchargée (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.
DEVOIR 13
1 exercice : Rédigez votre démarche en détail pour cet exercice. L’évaluation portera sur la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits.
Exercice
Pierre part en train de Bordeaux à 8h45min. Il arrive à Montpellier à 13h20min. Il se promène dans la ville pendant 2h15min puis repart en train pour Nice où il arrive à 18h34min.
Combien de temps en tout a-t-il passé dans un train au cours de cette journée ?
DEVOIR 14
1 exercice : Rédigez votre programme de construction en détail pour cet exercice. L’évaluation portera sur la qualité des consignes fournies : voir ci-dessus les détails concernant l’évaluation des écrits.
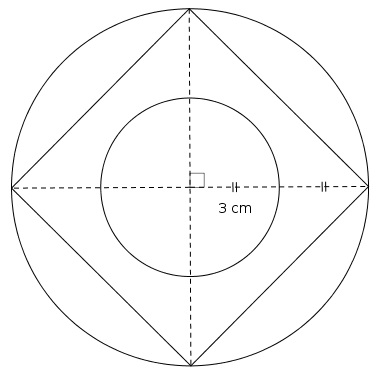
Exercice
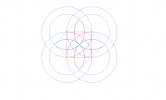
Rédiger un programme de construction de la figure suivante :
DEVOIR 15
1 exercice : Rédigez votre démarche en détail pour cet exercice. L’évaluation portera sur la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits.
Exercice
Pour quatre personnes, il faut 240 g de riz. Avec ces proportions :
a) Combien en faut-il pour 6 personnes ?
b) Combien de personnes peut-on servir avec 840 g de riz ?
DEVOIR 16
Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.
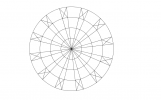
Tracer un cercle de centre A et de rayon 8 cm.
Placer 24 points B, C, D, ... sur ce cercle répartis de sorte que les angles au centre soient alternativement égaux à 10° et à 20°.
Ainsi, on aura $\widehat{BAC}$ = 10°, $\widehat{CAD}$ = 20°, …
Tracer 3 cercles concentriques de centre A et de rayons 2 cm, 4 cm et 6 cm.
Le cercle de rayon 6 cm coupe les rayons [AB] et [AC] aux points M et N respectivement. Tracer les segments [BN] et [CM]. Recommencer la même construction dans les autres angles de 10°.
DEVOIR 17
Ce devoir est à réaliser sur une feuille blanche (indiquez votre prénom, votre nom, votre classe et votre auto-évaluation).
L’évaluation portera sur la qualité des tracés : voir ci-dessus les détails concernant l’évaluation des constructions.
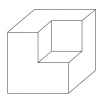
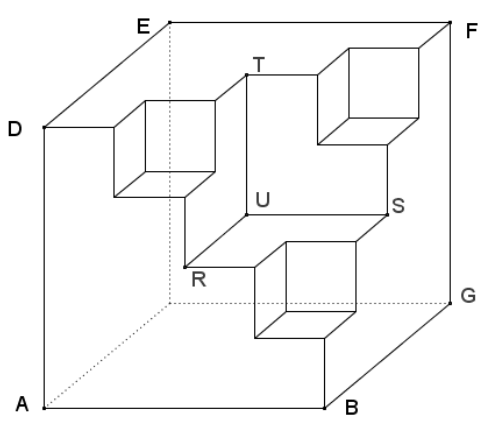
Il s’agit d’agrandir la figure ci-dessous qui représente un cube en perspective cavalière dont on a coupé certains coins. Pour cela, on tracera d’abord un carré ABCD de côté 12 cm puis un parallélogramme CDEF avec DE = 7 cm, $\widehat{CDE}$ = 40°, (CD)Â //Â (EF) et (CF)Â //Â (DE). On terminera la perspective cavalière par le tracé du parallélogramme BCFG avec (BC)Â //Â (GF) et (BG)Â //Â (CF).
Ensuite, voici quelques indications :
*Pour enlever un premier coin au cube, on repère les milieux M, N et P respectifs de [DC], [CF] et [CB] puis on trace 2 droites dont l’une est parallèle à (CB) et passe par M et l’autre parallèle à (DC) et passe par P ; ces 2 droites ont un point d’intersection qui est le point R. On procèdera de même pour obtenir les points S et T. Pour obtenir le point U, on suffit de faire en sorte que (RU)Â //Â (MT) et (TU)Â //Â ((MR).
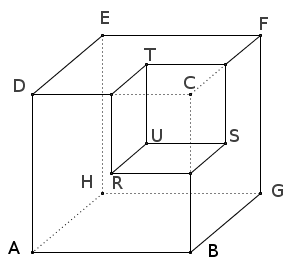
↠on a enlevé un coin
…et si on enlevait d’autres coins ?
DEVOIR 18
2 exercices : Rédigez votre démarche en détail pour le premier exercice. L’évaluation portera sur la qualité des explications fournies : voir ci-dessus les détails concernant l’évaluation des écrits.
Exercice 1
Le prix de 5 kg de girolles est de 320 €.
a) Quelles sont les 2 grandeurs de cette situation ? On admettra pour la suite qu’elles sont proportionnelles.
b) Combien coûtent 3 kg de girolles ?
c) Quelle masse de girolles peut-on acheter avec 40 € ?
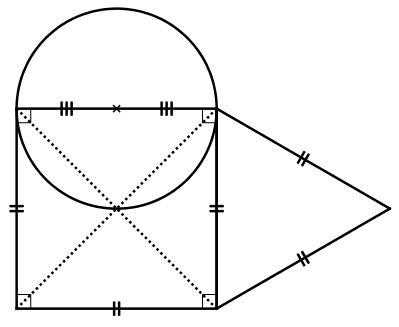
Exercice 2
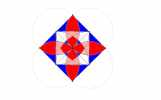
Rédiger un programme de construction de la figure suivante :
Documents joints
devoir n°15 - PDF - 225.2 ko