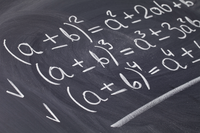
Les identités remarquables
Théorème
Pour tout nombre $a$ et $b$,
($a$+ $b$)²=$a$²+2$ab$+$b$²
($a$−$b$)²=$a$²−2$ab$+$b$²
($a$+$b$)($a$−$b$) = $a$²−$b$²
Démonstration
Soit 2 nombres $a$ et $b$, développons (a+b)² :
($a$+$b$)² = ($a$+$b$)($a$+$b$) = $a$²+$ab$+$ba$+$b$² = $a$²+2$ab$+$b$²
De même pour ($a$−$b$)² :
($a$−$b$)² = ($a$−$b$)($a$−$b$) = $a$²−$ab$−$ba$+$a$² = a²−2$ab$+$b$²
Et enfin, pour ($a$+$b$)($a$−$b$) :
($a$+$b$)($a$−$b$) = $a$² −$ab$+$ba$ −$b$² = a²−$b$² CQFD
