
Trigonométrie
Théorème
Pour tout triangle rectangle, les quotients de deux côtés ne dépendent que des angles aigus de ce triangle.
Plus précisément, ce théorème signifie que lorsqu’on divise deux côtés d’un triangle rectangle, le résultat ne dépend pas de la taille du triangle : on peut agrandir ou réduire le triangle sans que le quotient ne change.
Chaque quotient de deux côtés a reçu un nom mais il est d’usage actuellement de ne considérer que ceux l’on nomme sinus, cosinus et tangente. Les autres, qui sont les inverses de ces quotients, se nomment cosécante, sécante et cotangente.
Définitions
Pour tout triangle rectangle,
- Le sinus d’un angle aigu est égal au quotient du côté opposé par l’hypoténuse.
- Le cosinus d’un angle aigu est égal au quotient du côté adjacent par l’hypoténuse.
- La tangente d’un angle aigu est égal au quotient du côté opposé par le côté adjacent.
Démonstration
Soit deux triangles rectangles qui ont les mêmes angles mais des tailles différentes. Comme ils ont les mêmes angles, on peut les superposer de façon à obtenir la figure suivante :
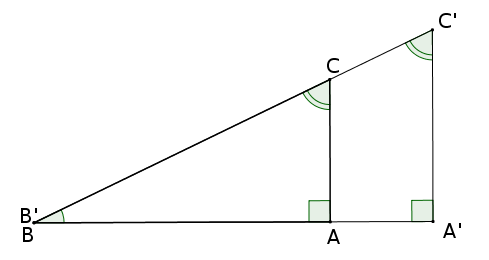
Sur cette figure, on a nommé les sommets des triangles pour que la démonstration soit plus facile à suivre. Ainsi, on a deux triangles $ABC$ et $A’B’C’$ rectangles en $A$ et en $A’$ avec $\widehat{ABC} = \widehat{A’B’C’}$ et $\widehat{ACB} = \widehat{A’C’B’}$ et emboîtés de sorte que $B = B’$ avec les alignements $B$, $A$, $A’$ et $B$, $C$, $C’$.
Par ailleurs, $(AC)$ et $(C’A’)$ sont perpendiculaires à $(BA’)$ donc $(AC)$ et $(C’A’)$ sont parallèles.
On peut donc utiliser le théorème de Thalès : $\dfrac{AB}{A’B’} = \dfrac{CB}{C’B’} = \dfrac{AC}{A’C’}$
– Avec les deux premières fractions égales, on obtient $AB \times C’B’ = A’B’ \times CB$
d’où $\dfrac{AB}{CB} = \dfrac{A’B’}{C’B’}$
ce qui montre que les quotients des côtés adjacents des angles $\widehat{ABC}$ et $\widehat{A’B’C’}$ (qui sont égaux) par les hypoténuses donnent bien le même résultat : cela ne dépend donc pas de la taille du triangle mais de ses angles.
– De même avec la 1ère fraction et la 3ème fraction égales, on obtient $AB \times A’C’ = AC \times A’B’$
d’où $\dfrac{AC}{AB} = \dfrac{A’C’}{A’B’}$
donc les quotients des côtés opposés des angles $\widehat{ABC}$ et $\widehat{A’B’C’}$ (qui sont égaux) par les côtés adjacents donnent bien le même résultat : cela ne dépend donc pas de la taille du triangle mais de ses angles.
– Enfin, avec la deuxième fraction et troisième fraction égales, $CB \times A’C’ = AC \times C’B’$
d’où $\dfrac{A’C’}{C’B’} = \dfrac{AC}{BC}$
donc les quotients des côtés opposés des angles $\widehat{ABC}$ et $\widehat{A’B’C’}$ (qui sont égaux) par les hypoténuses donnent bien le même résultat : cela ne dépend donc pas de la taille du triangle mais de ses angles.
Ainsi, dans chacun des cas, le quotient de deux côtés d’un triangle rectangle est égal au quotient des deux côtés correspondants de l’autre triangle rectangle, à condition qu’ils aient les mêmes angles aigus. CQFD
