
Angles opposés par le sommet
Définition
Deux angles sont opposés par le sommet quand ils ont le même sommet et quand les côtés de l’un sont dans le prolongement de côtés de l’autre.
Cette définition signifie que les côtés des angles opposés par le sommet forment deux droites sécantes ; et inversement, deux droites sécantes forment des angles opposés par le sommet.
Ainsi, dans la figure suivante, on a des angles opposés par le sommet :
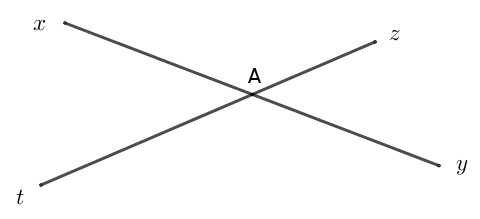
- $\widehat{xAt}$ et $\widehat{yAz}$ sont opposés par le sommet (repérés en bleu avec un seul arc de cercle ci-dessous)
- $\widehat{xAz}$ et $\widehat{yAt}$ sont opposés par le sommet (repérés en orange avec deux arcs de cercle ci-dessous)


Théorème
Deux angles opposés par le sommet sont égaux.
Ainsi, en reprenant les figures ci-dessus, on a : $\widehat{xAt}$ = $\widehat{yAz}$ et $\widehat{xAz}$ = $\widehat{yAt}$.
Démonstration
Soit 2 angles opposés par le sommet. Nommons-les $\widehat{xAt}$ et $\widehat{yAz}$ avec A le sommet commun.

Considérons l’angle $\widehat{yAt}$.

Par définition des angles opposés par le sommet, A est sur la droite $(xy)$ donc l’angle $\widehat{xAy}$ qui est la somme des angles $\widehat{xAt}$ et $\widehat{tAy}$ est un angle plat dont la valeur est égale à 180°.
En conséquence, on a : $\widehat{xAt}$ = 180° − $\widehat{tAy}$
De même, A est sur la droite $(tz)$ et un raisonnement similaire montre que $\widehat{zAy}$ = 180° − $\widehat{yAt}$
En comparant les deux égalités obtenus, il en résulte que $\widehat{xAt}$ = $\widehat{zAy}$ et donc les angles opposés par le sommet sont égaux CQFD.
